DATE:
Re: ERRORS THAT
CAN BE AVOIDED IN
This talk was not
an expose of the geostatistical ore reserve technique but rather a
philosophical discourse on the nature of misconceptions which occur in ore
reserve calculation procedures and their relative significance. A number of
points of interest were made and these are briefly given here not only as a
matter of record but to inform staff of these basic misconceptions and ways of
assessing the significance of assay data. I guess many of the points are
obvious but bear thinking about.
Geostatistical
(or any other technique for that matter) ore reserve estimation requires some
training, but recognising calculations based on faulty principals or wishful
thinking takes only a few minutes to learn and three basic principals only
should be accepted. These are given later.
For successful
development and mining of an ore body the ore reserve estimation must be
reliable and progressive based on good sampling and calculation techniques, the
"flow" of reserve estimation over the life of a deposit may be
summarised as follows:
![]()
![]() GOOD DEPOSIT
GOOD DEPOSIT
GOOD SAMPLING
GOOD
TOTAL RESERVE
CALCULATION (GEOLOGICAL)
![]() GOOD
RECOVERABLE
GOOD
RECOVERABLE
RESERVE CALCULATION
![]()
GOOD GRADE CONTROL
PROGRAMME
Inherent in the
discovery of a good deposit based on a successful drilling programme is the
"psychological bias" i.e. "successful drilling tends to bias
reserve estimates towards higher tonnages and grade" and a corollary of
this that "ore reserve estimation is not simply a matter of converting
various intersection lengths and assays to tonnage and grade whether by hand or
delegating the task to a black box", (after Haddon King).
The basic
principles, which should be addressed, are:
1) SAMPLE VALUE
DETERMINED BY A LABORATORY IS NOT THE GRADE OF THE CORE BUT THE VALUE OF THE
SAMPLE ASSAYED.
For example, a
20gm sample weight split from 20kgm of crushed and pulverised core is highly
likely to have a different value to a sample of weight 50gm or 500gm etc.
especially for say gold or similar low content element. Similarly, different
assay values from different crushed splits or repeat assays by different
laboratories of the same core interval may all be valid and correct for the
actual assayed samples, the differences reflecting original distribution of
material in core or how a limited number of grains have distributed themselves
in the pulps prepared for assay. None are necessarily wrong, (or right!).
Probably average of all values is closer to the true value.
2) GRADE OF CORE
IS NOT GRADE OF STOPE OR ASSAY BLOCK FROM WHICH THE CORE WAS EXTRACTED.
Relevance of core
is often over rated. In fact it can be said a given length of core does not
represent that block of ground it came from ie that
particular bit of rock is no longer in the ground, and it is the value of that
which is left to be mined that is important not what is sitting in the core
shed. Again this is more important for precious metals than say a volcanogenic
sulphide deposit, for example what value do you place on say a 200g/t Au assay
value in a section of core in a given drill hole when a nearby drill hole
assays 0.2g/t ie does the 200g/t assay value reflect
a single small grain fortuitously picked up in the assayed sample split or does
the 0.2g/t value mean that the cored interval just missed a large 200g/t but
irregularly mineralised zone etc.
An example of how
core assay variability influences reserve estimation is, taken from a gold mine
in
Zone of high
gold assays AQ core Zone of high
gold assays PQ core PQ core –
12.19m @ 4.82g/t = 58.76m-g AQ
core – 9.14m @ 5.85g/t = 53.47m-g
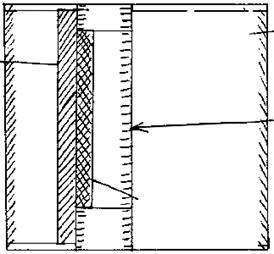
Both metre-gram
(m-g) values are similar but in terms of mining and assessing a
mineable reserve which is most valid to use eg. taking mining cost into consideration, is it better to base
reserve on the 9 metre intersection or 12m intersection value? It may not be economically viable to mine the
12m section because of the necessarily larger plant size requirements etc. to
cater for larger reserve etc.
3) GRADE IS NOT
RANDOMLY DISTRIBUTED
This is a basic
tenet of geostatistical ore reserve estimation in that the assumption is made,
supported by empirical and actual observation, that there are systematic and
statistically quantifiable changes in the distribution of any mineralisation,
for example, high grade zones are surrounded by lower grade zones etc., or a
high grade block is likely to be surrounded by lower grade blocks.
The grade
variation may be "ordered" by means of a variogram plot, which is a
function of the sample interval, and serves to smooth and determine rate of
variability. For example, "waste" may only be waste because a
particular drill hole in a given block is low, but it may in fact be ore i.e.
too much reliance on a given bit of core or blast hole assay value and not
attributing enough weighting to ore distribution trends and variation through
the ore body. That is, a "low"
zone surrounded by ore is more likely to be a "low assay" from the
ore zone and not barren rock, unless there is a particular geological reason
why a given site should be low or barren.
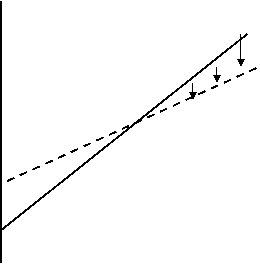
Within a
mineralised zone the use of the variogram to determine grade has the affect of
increasing lower grade values and decreasing the higher-grade values i.e.
values trend towards the average. This is observed in practice during mining
i.e. the recovered grades in lower grade sections tend to be higher than
anticipated from drilling and lower in higher grade sections.
![]()
![]()
![]() real
real
![]() recovered
recovered
![]() grade
grade
![]()
![]()
estimated
value
Choice of sample
is important to get good statistics because grade of sample used is not
necessarily representative of the block from which it came. This is a reflection of numbers of grain
particles assayed, for example would need 20 gold particles/assay sample (10gm)
to get a 20% precision; (about 10,000 particles to give 1% precision), often a
highly unlikely occurrence.
As an example,
best grade control technique at an open pit Au mine in
From elsewhere
Professor Krige has discussed the problem of defining
the degree of uncertainty in grade estimates based on borehole data from new
discoveries. He states that even if the property does not form the extension of
an existing ore-field, as for example in the